| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 |
Tags
- 창작수하
- 미스터리스릴러
- 스릴러
- 정십이면체부피
- 덧셈문제
- 타원 넓이증명과 풀이
- 순간반사능력상승
- 하늘나비
- 명언으로 배우는 중국어
- 서울아타트
- 사랑과배신
- 곱셈12단카드게임
- 창작 이야기
- 아베신조사과
- 타원 둘레
- 집중력상승
- 정치코믹풍자
- 정십이면체겉넓이
- 창작이야기
- 영어
- 뺄셈
- 암기력상승
- 명언
- 중국어
- 경제풍자코믹
- 화장실에서 잠깐 영어공부하기
- 곱셈12단게임
- 정십이면체높이
- 미스터리
- 신경제도시
Archives
- Today
- Total
하늘나비의 소소한 창작이야기1-수학이야기-
하늘나비의 다면체-뿔과 다면체- 본문
연구저자 하늘나비.












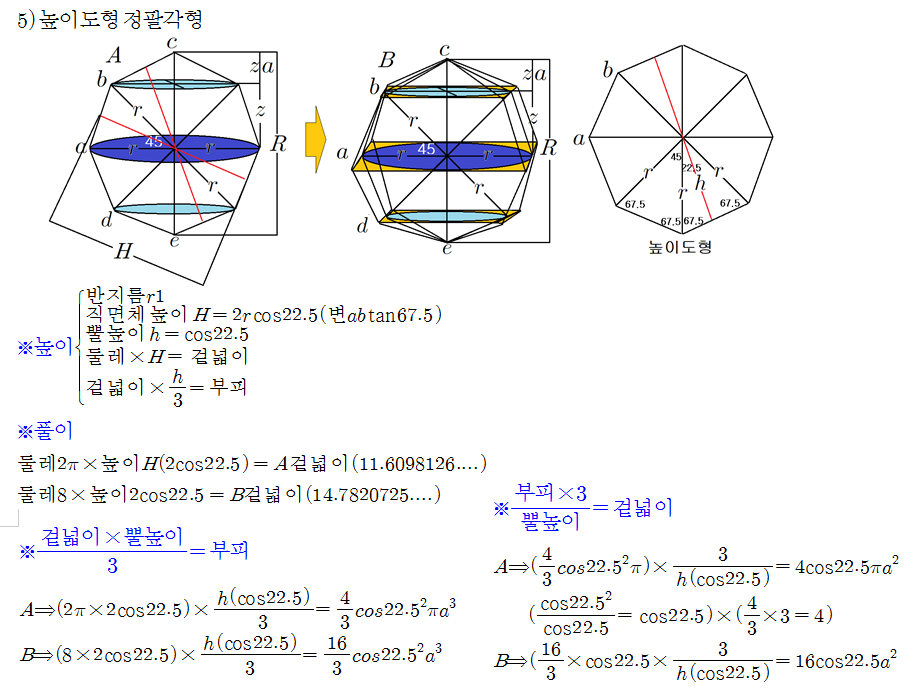
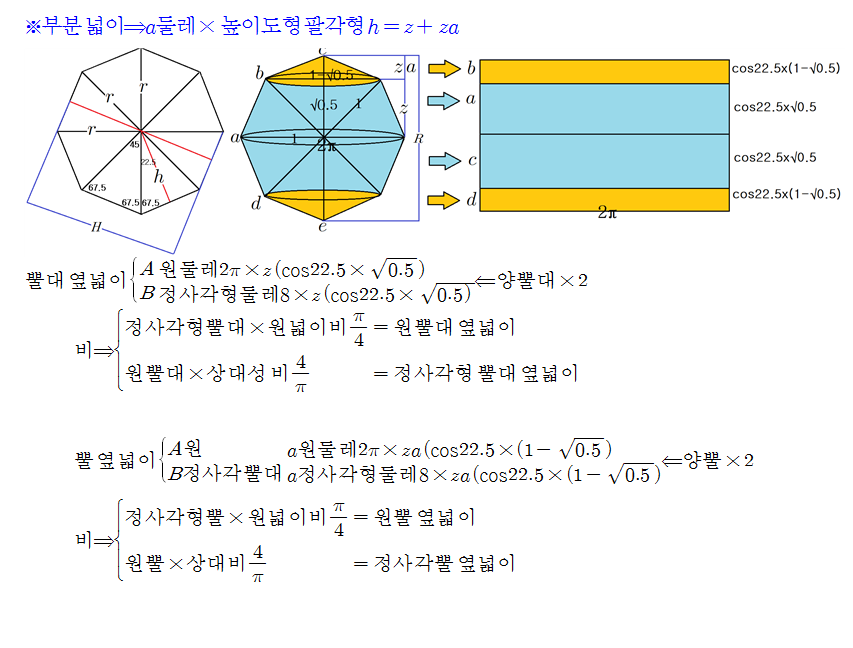
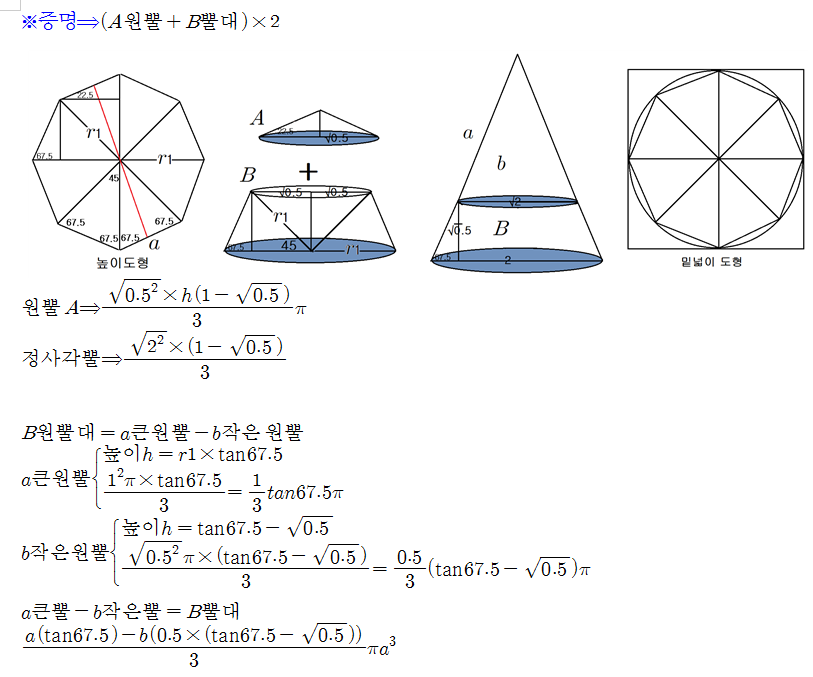







구를 평면으로 잘라냈을 때, 지름 기준으로 원이 전체 면적을 감싸게 되며, 다시 원을 360도 회전시켜 끼워놓게 되며, 구가 된다. A구에서 색칠된 원을 잘라냈을 때 비스듬한 원이 만들어지며, 평면으로 고정시켜주게 될 때, B-b인 원이 된다. 평면 구처럼 원의 지름은 모두 같으며, 둘레를 무한으로 잘라내 다시 B-b로 수평으로 쌓게 된다. 이때 원 높이는 0이다. 겉넓이에 조건은 둘레⨯높이다. 여기서 둘레Rπ⨯높이0→0=R로 변형된다. 어디를 선택해도 높이는 R이다.
이런 형태로 계속 쌓게 될 때 원통이 된다.
r⨯2=R(지름)
'창작수학' 카테고리의 다른 글
| 곡선비율 (0) | 2019.11.07 |
|---|---|
| 곡선과 타원곡선 (0) | 2019.11.07 |
| 타원둘레유도하기 (0) | 2019.11.07 |
| 점에 대해 정의내리다. 연구저자 하늘나비. (0) | 2019.06.14 |
| 타원 유도-연구저자. 하늘나비 (0) | 2019.06.08 |
Comments




