| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 |
- 곱셈12단게임
- 명언
- 창작수하
- 뺄셈
- 암기력상승
- 창작이야기
- 미스터리스릴러
- 중국어
- 화장실에서 잠깐 영어공부하기
- 서울아타트
- 사랑과배신
- 아베신조사과
- 정십이면체겉넓이
- 하늘나비
- 미스터리
- 창작 이야기
- 정치코믹풍자
- 집중력상승
- 순간반사능력상승
- 신경제도시
- 영어
- 타원 넓이증명과 풀이
- 정십이면체높이
- 경제풍자코믹
- 곱셈12단카드게임
- 덧셈문제
- 정십이면체부피
- 명언으로 배우는 중국어
- 스릴러
- 타원 둘레
- Today
- Total
하늘나비의 소소한 창작이야기1-수학이야기-
하늘나비 우주 양면이론 테스트1-1. 블랙홀과 푸앵카레의 추측... 본문
블랙홀이 양 쪽으로 원뿔형으로 이루어졌다고 추측하게 될 때 아래와 같이 블랙홀을 한 점으로 압축이 가능하다

A그림이 블랙홀이라고 할 때, a공간은 구 부피 공간이 되며, 원뿔 공간은 빈공간이 된다. 물론, 부피질량 a=b≧0 & F≧0
A원기둥 옆넓이 Rrπ= B반구 겉넓이 Rrπ
A원기둥 a부피 r²rπ-r²r/3π=B반구 부피4r²r/6π
따라서 A공간=B공간
푸앵카레의 추측을 풀어보자.
A는 그대로 놔두고 B를 뒤집어주게 된다.

러시아인이 푼 푸앵카레의 추측을 참고“
구에 끈을 구를 감고 당길 때 끈은 F 점으로 내려오게 되므로 한 점이 된다.
B구를 한 쪽 방향으로 지름 값으로 팽창시켰을 때 A 구멍뚫인 원기둥이 만들어진다. 이때 다시 원뿔 나선형으로 F점에 모이게 되므로 블랙홀(도넛형)과 구형(사과)는 모두 한 점으로 모이게 되므로 우주는 두 종류로 이루어졌다고 정리할 수 있다.

A도형을 F점 기준으로 일정한 방향으로 압축시킬 때 직선이 남게 된다. C직선은 뿔과 같다.
2차원 면적으로 설명하기.
A꼭짓점은 0이라고 할 때, F점 부분 밑넓이와 반구 원넓이는 같으며,
A윗면은 빈 공간이므로 반구F점과 같다. 즉, A에 끈을 당길 때 F점이 된다.
모든 도형은 구형이 아닌 뿔형으로 이루어졌다.
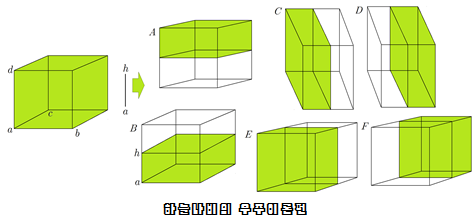
C(r)=ad라고 할 때, 직선ah는 ad/2일 때, 그림 ABCDEF처럼 ah직선을 채워놓아야 한다. 직선이 육면체라고 할 때, 밑넓이×높이가 된다.
따라서
ab2, ac2, ad2라고 할 때, ha=(ad/2=1)
ab×ac×ha×6=2×2×1×6=24
정육면체 부피는 a³=2³
따라서 직선 ah는 육면체보다 작다.
ab×ac×ha×⅓×6=2×2×1×⅓×6=8
정육면체 부피와 동일해진다.
따라서 ab×ac×ha×⅓은 뿔이므로 직선ah는 뿔이라고 정리할 수 있다.
하늘나비의 구 겉넓이, 부피 풀이 증참조.
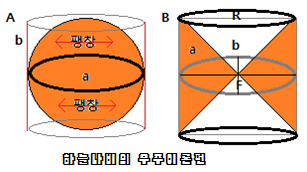
a공간은 구 공간이며, b공간은 현재 암흑물질 공간, 현재 우주 공간이다. a공간은 미지의 공간, 우주 밖 공간이 되며, a공간에서 현재의 질량, 물질을 보급하고 있다.
우리 우주는 a공간이 아닌 b공간에 존재하며, 양 뿔을 기준으로 두 개의 우주 공간이 만들어진다. 이것을 양면우주라고 한다.
또한, 꼭짓점F0일 때, 팽창된 b공간도 0이 된다. 따라서 아무리 원둘레 지름R이 크더라도 공간은 0이므로 꼭짓점F와 같다. 따라서 무한으로 팽창압축이 가능하게 된다.

AF 꼭짓점 공간과 BF공간 모두 0이다. 이것을 그대로 푸앵카레의 추측에다가 적응해보자. A는 구라고 할 때, B는 도넛 형이 된다. 즉 두 개 다 한 점에 모이게 된다. 또한, 현실에서도 잘 나타내주고 있다. 블랙홀과 행성들 이렇게 우주는 두 개를 기본 형태로 이루어졌다. 따라서 전체 우주는 팽창을 거듭하고 있다는 점을 볼 때, 위 그림과 같은 형태로 이루어질 가능성이 매우 높다.

구와 도넛을 구분할 때, 구형태에다가 끈을 묶어서 당길 때 한 점으로 모인다. 그러나 A도넛형을 안쪽으로 압축시켰을 때 어떻게 될 까? B공간은 0이며, BF공간 0이다. 단지 다른 점이 있다면 폭 길이 즉, 공간 넓이 차이다. 이것은 어디까지나 인간들이 확인할 수 있는 예일 뿐이다. 블랙홀을 생각해보면 쉬울 듯하다. 블랙홀이 꼭짓점으로 이루어졌는지 A처럼 커다란 넓이로 존재하는 지를. 그러나 아쉽게도 블랙홀 안으로 들어갈 수도 없으며 확인할 수도 있다. 그렇다고 빈공간이 사라진 것이 아니다. 꼭짓점F공간은 빈 공간이므로 A 도넛 안쪽 공간0=압축된 F공간0이므로 둘의 값은 일치하다.
그럼 B형태의 구멍이 뚫린 도넛모양과 구를 어떻게 구분할 것인가? B구멍뚫인 공간 F 값은 1-(⅓+⅓+⅓)>0이다.
따라서 푸앵카레의 추측 자체가 오류가 존재할 가능성이 매우 높다. 애당초 시작점이 구형태라고 단정 짓는 자체가 위험하지 않을까한다. 두 종류로 이루어졌을 가능성이 매우 높다. 그 예로 음과 양을 예로 들 수 있다. 두 개의 기본 값을 기본으로 현 우주가 만들어지게 된다.
